数学分析 - 数列

数列极限的定义

数列：$\alpha_{1},\alpha_{2},\dots,\alpha_{n},\dots$这样排成一列的实数称为数列。

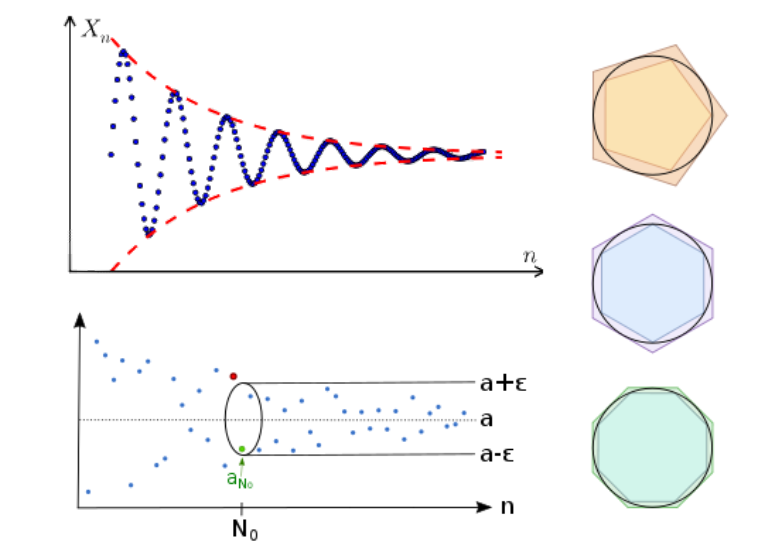
如果 $a_{n}$ 随着 $n$ 充分增大，逐渐接近为一个实数 $\alpha$ 时，称，数列 $\{\alpha_{n}\}$ 收敛于$\alpha$。

但是，“充分增大”，“逐渐接近”这些词是模糊不清，缺乏严谨的，应该避免使用。

很容易知道，如果 $\{\alpha_{n}\}$ 收敛于 $\alpha$，说明，随着 $n$ 的增大，$\alpha_{n}$ 与 $\alpha$ 的距离会越来越小，即，无论我们取多么小的一个距离 $\varepsilon$，随着 $n$ 的增大，某一项 $n_{0}(\varepsilon)$ （可以由 $\varepsilon$ 决定，是一个关于 $\varepsilon$ 的表达式）之后，$\alpha_{n}$ 与 $\alpha$，之间的距离总会比这个距离还小。

这样的表述很好的避免使用含糊不清的词，仅用有限的正整数和实数表达出来了极限的概念。

极限与极限点

Definition: 数列的极限
设$\{\alpha_{n}\}$为一个数列，给定任意正实数 $\varepsilon$，当 $n>n_{0}(\varepsilon)$ 时，$|\alpha_{n}-\alpha|<\varepsilon$总是成立，那么称数列$\{\alpha_{n}\}$收敛，数列的极限为 $\lim_{ n \to \infty }\alpha_{n}=\alpha$。

为什么要用 $n_{0}(\varepsilon)$ 而不是 $N$：主要是为了显式体现出 $\varepsilon$ 与其的关系，某些地方省略也不影响时也会使用 $N$ 或直接 $n_{0}$

数列的极限不存在只有两种情况：

1. 数列发散（无界），即 $\lim_{ n \to \infty } \alpha_{n}=\infty$。
2. 数列在常数间震荡。
   （也有把 $\lim_{ n \to \infty } \alpha_{n}=\infty$ 视为极限存在，为无穷，数列不收敛）

---

Definition: 数列的聚点
在某点附近无论多么小的范围内，都有无限个项，数列$\{\alpha_{n}\}$，给定任意正实数$\varepsilon$， 如果满足 $|\alpha_{n}-\beta|<\varepsilon$ 的项有无穷个，则 $\beta$ 是 $\{\alpha_{n}\}$ 的一个聚点。

聚点只要求有无穷个项在该点附近，一个数列可能会有多个极限点。如果数列存在极限，则聚点有且只有一个，为该数列的极限（证明见下文）。

---

Theorem 1.1.1
数列$\{\alpha_{n}\}$ 收敛于 $\alpha$ 的充分必要条件是，任意给定满足$\rho<\alpha<\sigma$的 $\rho,\sigma$，除了有限个正整数 $n$ 以外（即除了$n\leq n_{0}(\varepsilon)$ 的部分） $\rho<\alpha_{n}<\sigma$ 都成立。

必要性证明 ($\impliedby$):
设 $\varepsilon=\min(\alpha-\rho,\sigma-\rho)$ ，是 $\rho$ 与 $\sigma$ 中与 $\alpha$ 最小的距离。显然

$\rho\leq \alpha-\varepsilon <\alpha+\varepsilon\leq \rho+\varepsilon$

根据定义，对于 $\varepsilon$ 存在$N$，使得 $n>N$ 时 $|\alpha_{n}-\alpha|<\varepsilon$，此时显然

$\alpha-\varepsilon<\alpha_{n}<\alpha+\varepsilon$

所以，只要 $n>N$，就满足$\rho<\alpha_{n}<\sigma$。

充分性证明 ($\implies$):
根据条件：$\alpha-\varepsilon< \alpha_{n}<\alpha+\varepsilon$，除了有限个正整数 $n$ 以外都成立。
取有限的不成立的 $n$ 中最大的一个为 $N$，则，当$n>N$时：

$-\varepsilon<\alpha_{n}-\alpha<\varepsilon \implies |\alpha_{n}-\alpha|<\varepsilon$

数列极限的性质

Theorem 1.1.2 唯一性
数列收敛，极限唯一

证明：如果数列 $\{\alpha_{n}\}$ 存在两个极限，$\alpha,\beta$，且$\alpha<\beta$，根据稠密性，存在$r$ 满足 $\alpha<r<\beta$。
根据定理 1.1，除有限个$n$外，满足$\alpha_{n}<r$，同时有$r<\alpha_{n}$，产生矛盾。

同时，数列收敛，极限点唯一：根据定理 1.1 易得。

Theorem 1.1.3 有界性
数列 $\{\alpha_{n}\}$ 收敛，则存在 $M \in \mathbb{R}^+$ 使得，对于任意 $n$ 都有，$\alpha_{n}<M$

证明：不妨取 $\varepsilon=1$，此时只要 $n>n_{0}(1)$，就有 $\alpha-1< \alpha_{n} < \alpha+1$，这无限个项是有界的，此时只需考虑剩下 $1\sim n$ 这些项，直接取 $M=\max\{|\alpha_{1}|,\dots,|\alpha_{n}|,|\alpha-1|,|\alpha+1|\}$，即可。

Theorem 1.1.4 保号性
设数列 $\{ \alpha_{n} \}$ 收敛于 $a$，若 $a>0$ 则任意 $a^\prime \in(0,a)$ 都存在$n_{0}\in \mathbb{N}^+$，当 $n>n_{0}$ 时，$\alpha_{n}>a^\prime$

证明：取 $\varepsilon=a-a^\prime$，则存在 $n_{0}(\varepsilon)>0$，只要 $n>n_{0}(\varepsilon)$ 就有 $|\alpha_{n}-a|<\varepsilon$，即 $\alpha_{n}>a-\varepsilon=a^\prime$。

$a<0$ 的情况同理。

柯西收敛准则

如果我们并不知道数列的极限是什么，此时该如何判断数列是否收敛？
如果一个数列收敛，因为都同接近某一个数，显然项与项之间的距离会越来越小，否则发散。

---

Theorem 1.2: 柯西收敛准则
$\alpha_{n}$收敛的充分必要条件是，$\forall \varepsilon,\exists n_{0}(\varepsilon)$，当$n>n_{0}(\varepsilon),m>n_{0}(\varepsilon)$时，$|\alpha_{n}-\alpha_{m}|<\varepsilon$

必要性证明 ($\impliedby$):
设 $\lim_{ n \to \infty }\alpha_{n}=\alpha$，$\forall \varepsilon$，对于$\frac{\varepsilon}{2}$，$\exists n_{0}\left( \frac{\varepsilon}{2} \right)$，当$n>n_{0}\left( \frac{\varepsilon}{2} \right),m>n_{0}\left( \frac{\varepsilon}{2} \right)$时，$|\alpha_{n}-\alpha|< \frac{\varepsilon}{2}$,$|\alpha_{m}-\alpha|< \frac{\varepsilon}{2}$，此时

$|\alpha_{n}-\alpha_{m}|=|\alpha_{n}-\alpha+\alpha-\alpha_{m}|\leq|\alpha_{n}-\alpha|+|\alpha_{m}-\alpha|<\varepsilon$

充分性证明 ($\implies$):
根据定理 $1.1$，如果 $\forall\rho<\alpha$ 则有至多有限个 $n$ 使得 $\alpha_{n}\leq \rho$ 成立。$\forall \rho>\alpha$，就有无限个 $n$ 使得 $\alpha_{m}\leq \rho$ 成立则数列收敛，依此进行证明。

• 证明
• 流程图

条件：存在正整数 $n_{0}(\varepsilon)$ 当 $n>n_{0}(\varepsilon),m>n_{0}(\varepsilon)$ 时，$|a_{n}-a_{m}|<\varepsilon$。

假设：

1. $A$ 为使 “只有有限个项满足 $\alpha_{n}\leq\rho$ ”，的所有 $\rho$ 的集合。
2. $A^\prime$，为$A$的补集，即为使得 “有无限个项满足 $\alpha_{n}\leq \sigma$”，的所有 $\sigma$ 的集合。

证明 $A$ 与 $A^\prime$ 非空：
取一正整数 $l >n_{0}(1)$，则只要 $n>n_{0}(1)$ 时，都有 $a_{l}-1<a_{n}<a_{l}+1$ ，因此 $a_{l}-1 \in A$，$a_{l}+1 \in B$ ，即 $A$ 与 $A^\prime$ 非空。

此时，$\langle A,A^\prime \rangle$ 是 $\mathbb{R}$ 的分划，显然 $\rho<\sigma$。

由于实数的稠密性，必定存在 $\alpha$ 满足 $\forall\rho \in A,\forall\sigma \in A^\prime,\rho<\alpha<\sigma$，又由于$\langle A,A^\prime \rangle$ 是 $\mathbb{R}$ 的分划，根据Dedkind 切割定理 所以 $\alpha$ 要么是 $A$ 中的最大数，要么是 $A^\prime$ 中的最小数。

证明满足定理 1.1.1：只需证明任意给定满足 $\rho<\alpha<\sigma$ 的 $\rho,\sigma$，除了有限个自然数 $n$ 以外 $\rho<\alpha_{n}<\sigma$ 都成立，即可证明数列收敛。

根据假设 1 ，满足 $\alpha_{n}\leq\rho$ 的项有有限个，即 $\rho<\alpha_{n}$ 除了有限个项外都成立。

任意给定 $\sigma \in A^\prime$ 根据有理数的稠密性，可以选取一个 $r$ 满足 $\alpha<r<\sigma$，令$\varepsilon=\sigma-r$，此时对于 $\varepsilon$ 存在 $n_{0}(\varepsilon)$，使得 $n>n_{0}(\varepsilon),m>n_{0}(\varepsilon)$ 时，$|\alpha_{n}-\alpha_{m}|<\varepsilon =\sigma-r$，成立。

$r>\alpha$ 所以 $r \in A^\prime$，因此，有无数个正整数 $m$ 使得 $\alpha_{m}\leq r$ 成立，显然在这无数个 $m$ 中也存在无数个满足 $m>n_{0}(\varepsilon)$

一旦从这无数个 $m$ 中确定一个，此时只要 $n>n_{0}(\varepsilon)$ 就有 $a_{n}-a_{m}<\sigma-r$，又 $\alpha_m\leq r$ 所以 $\alpha_n<\sigma$ 。综上 $\alpha_{n}<\sigma$ 除了有限个项外都成立。

以上，除了有限个$n$外，不等式$\rho<\alpha_{n}<\sigma$ 成立，满足定理$1.1.1$。

数列之间的关系

Theorem 1.3.1 保不等式性
数列$\{a_{n}\}$，$\{\beta_{n}\}$ 收敛，对无数个正整数 $n$ 都有 $\alpha_{n}\leq \beta_{n}$ 那么 $\lim_{ n \to \infty }\alpha_{n}\leq \lim_{ n \to \infty } \beta_{n}$

证明：
假设$\lim_{ n \to \infty } \alpha_{n}=\alpha$，$\lim_{ n \to \infty } \beta_{n}=\beta$ 。
如果 $\alpha>\beta$ ，可以找到一个 $r$ 满足 $\alpha>r>\beta$ ，根据定理 1.1.1，除有限个$n$外，都有$\alpha_{n}>r$，同时$\beta_{n}<r$，可得$\beta_{n}<r<\alpha_{n}$，与$\alpha_{n}\leq \beta_{n}$ 相矛盾。

推论：数列$\{\alpha_{n}\}$收敛，对无穷个$n$，都有$\alpha_{n}\leq \rho$，那么$\lim_{ n \to \infty }\alpha_{n}\leq \rho$

---

Theorem 1.3.2 极限四则运算法则
列$\{\alpha_{n}\}$，$\{\beta_{n}\}$ 收敛，则数列$\{\alpha_{n}+\beta_{n}\}$，$\{\alpha_{n}\cdot \beta_{n}\}$ 也收敛，且

$\begin{aligned} \lim_{ n \to \infty }(\alpha_{n}+\beta_{n})=\lim_{ n \to \infty}\alpha_{n}+\lim_{ n \to \infty }\beta_{n} \\ \lim_{ n \to \infty }(\alpha_{n}\cdot\beta_{n})=\lim_{ n \to \infty}\alpha_{n}\cdot\lim_{ n \to \infty }\beta_{n} \end{aligned}$

加减的证明：
设 $\lim_{ n \to \infty }\alpha_{n}=\alpha$，$\lim_{ n \to \infty } \beta_{n}=\beta$
任意给定的正实数 $\varepsilon$，对 $\frac{\varepsilon}{2}$ 有$n_{\alpha}\left( \frac{\varepsilon}{2} \right) \in \mathbb{N}^+,n_{\beta}\left( \frac{\varepsilon}{2} \right)\in\mathbb{N}^+$，只要$n>\max\left\{ n_{\alpha}\left( \frac{\varepsilon}{2} \right),n_{\beta}\left( \frac{\varepsilon}{2} \right) \right\}$ 时，$|a_{n}-\alpha|< \frac{\varepsilon}{2}$，$|\beta_{n}-\beta|< \frac{\varepsilon}{2}$成立，因此

$|\alpha_{n} +\beta_{n}-\alpha-\beta|\leq |\alpha_{n}-\alpha|+|\beta_{n}-\beta|\leq \varepsilon$

所以 $\{\alpha_{n}+\beta_{n}\}$ 收敛于$\alpha+\beta$ ，$\{\alpha_{n}-\beta_{n}\}$同理

乘除的证明：

$|\alpha_{n}\beta_{n}-\alpha\beta|=|(\alpha_{n}-a)\beta_{n}+(\beta_{n}-\beta)a |\leq|\alpha_{n}-\alpha||\beta_{n}|+|\beta_{n}-\beta||a|$

又由于收敛数列是有界的（定理1.1.3），即存在正实数 $M$，使得 $\forall n\in\mathbb{N}^+$ 都 $\beta_{n}\leq M$ 。
任意给定的正实数 $\varepsilon$，只要$n>\max\left\{ n_{\alpha}\left( \frac{\varepsilon}{2M} \right),n_{\beta}\left(\frac{\varepsilon}{2|a|}\right) \right\}$ 时，$|a_{n}-\alpha|< \frac{\varepsilon}{2M}$，$|\beta_{n}-\beta|< \frac{\varepsilon}{2|a|}$成立，此时

$|\alpha_{n}\beta_{n}-\alpha\beta|\leq \frac{\varepsilon}{2M}|\beta_{n}|+\frac{\varepsilon}{2|a|}|a|\leq \varepsilon$

同理，只要 $\beta_{n}\neq 0$ 且 $\lim_{ n \to \infty } \beta_{n}\neq 0$ 则 $\lim_{ n \to \infty } \frac{\alpha_{n}}{\beta_{n}}=\frac{\lim_{ n \to \infty }\alpha_{n}}{\lim_{ n \to \infty }\beta_{n}}$

Theorem 1.3.3 迫敛性
数列 $\{ \alpha_{n} \}$ $\{\beta_{n}\}$ 收敛于 $a$，数列 $\{ \gamma_{n} \}$ 满足，存在 $N_{0} \in \mathbb{N}^+$ 当 $n>N$ 时有 $\alpha_{n}\leq \gamma_{n}\leq \beta_{n}$

根据极限的四则运算（定理 1.3.2）可知 $\lim_{ n \to \infty }\alpha_{n}-\beta=0$
任意给定正实数 $\varepsilon$ 存在 $n_{0}(\varepsilon) \in\mathbb{N}^+$ 只要 $n>\max\{ n_{0}(\varepsilon),N_{0} \}$ 时，就有

$|\alpha_{n}-\beta_{n}|=|\alpha_{n}-\gamma_{n}+\gamma_{n}-\beta_{n}|\leq|\alpha_{n}-\gamma_{n}|+|\gamma_{n}-\beta_{n}|\leq |\gamma_{n}-a| \leq \varepsilon$

Theorem 1.3.4: 致密性定理
有界数列一定有收敛子列

见平面中的致密性定理证明（定理 2.4.5）。

---

**Theorem 1.3.5
数列$\{\beta_{n}\}$ 是 $\{\alpha_{n}\}$ 的一个子列，若 ${\beta_{n}}$ 存在极限点 $\beta$ ，则 $\beta$ 也是 $\{\alpha_{n}\}$ 的一个极限点。

显然 $\beta$ 附近有无数个 $\beta_{n}$，又 $\beta_{n}$ 也是 $\{ \alpha_{n} \}$ 的项，所以 $\beta$ 附近也有无数个 $\alpha_{n}$，即 $\beta$ 也是 $\alpha_{n}$ 的一个极限点。

---

Theorem 1.3.6
收敛数列的任意子列也收敛，且极限相同。

上下（左右）极限

显然，$\{\alpha_{n}\}$ 删除有限个项后得到的子数列 $\{\alpha_{m_{n}}\}$ 收敛于相同的极限。

由定理 $1.1$ 易得：

• 有上界的单调非减数列收敛于上界
• 有下界的单调非减数列受限于下界

上下极限的定义

Definition: 下极限
有界数列 $\{a_{n}\}$，去除开始的 $m$ 项，把剩余的 $\alpha_{m+1},\dots,\alpha_{m+n},\dots$的下界设为 $\beta_{m}$

$\beta_{m}=\inf_{n>m}\alpha_{n} \Longleftrightarrow \min\{\alpha_{m+n}\}$

极限 $\lim_{ m \to \infty } \beta_{m}=\beta$ 称为 $\alpha_{n}$ 的下极限，记为 $\liminf_{n\to \infty} {\alpha_{n}}$或\varliminf_{n\to \infty} {\alpha_{n}}。

显然：

1. $i>j$ 时，$\beta_{i}\geq\beta_{j}$，单调非减，且有上界，所以 $\{\beta_{m}\}$ 收敛。
2. $\{\beta_{m}\}$ 是 $\{\alpha_{n}\}$ 的一个子列
3. 只要数列有界，就有下极限

且有性质：对于任意正实数 $\varepsilon$

1. 使得 $\alpha_{n}\leq \liminf_{n\to \infty}\alpha_{n} - \varepsilon$ 成立的项至多有有限个。
2. 使得 $\alpha_{n}< \liminf_{n\to \infty}\alpha_{n}+\varepsilon$ 成立的项有无数个。
   换言之，$\liminf_{n\to \infty}\alpha_{n}$ 是数列 $\{\alpha_{n}\}$ 的最小极限点。

1 的证明：
设 $\lim_{ m \to \infty } \beta_{m}=\beta$，给定任意正实数 $\varepsilon$，存在自然数$m_{0}(\varepsilon)$，使得 $m>m_{0}(\varepsilon)$ 时，$|\beta_{m}-\beta|<\varepsilon$ 成立，由于 $\{\beta_{m}\}$ 单调非减，$\beta_{m}>\beta-\varepsilon$ 成立。

由于$\beta_{m}=\inf_{n>m} \alpha_{n}$ ，所以当 $n>m$ 时，则 $\alpha_{n}\geq \beta_{m}>\beta-\varepsilon$，换言之，只有 $m\leq n$ 时，$\alpha_{n}<\beta - \varepsilon$。

2 的证明 ：
设 $\lim_{ m \to \infty } \beta_{m}=\beta$，由于 $\{\beta_{m}\}$ 是 $\{\alpha_{n}\}$ 的一个子列，根据定理 $(5)$，$\beta$ 也是 $\{\alpha_{n}\}$ 的一个极限点，即给定任意正实数 $\varepsilon$，有无穷个项满足 $|\alpha_{n}-\beta|<\varepsilon$，即有无穷个项满足 $\alpha_{n}<\beta+\varepsilon$。

---

Definition: 上极限
同理，有界数列 $\{a_{n}\}$，去除开始的 $m$ 项，把剩余的 $\alpha_{m+1},\dots,\alpha_{m+n},\dots$的上界设为 $\beta_{m}$

$\beta_{m}=\sup_{n>m}\alpha_{n} \Longleftrightarrow \max\{\alpha_{m+n}\}$

极限 $\lim_{ m \to \infty } \beta_{m}=\beta$ 称为 $\alpha_{n}$ 的上极限，记为 $\limsup_{n\to \infty} {\alpha_{n}}$或\varlimsup_{n\to \infty} {\alpha_{n}}。

给定任意正实数$\varepsilon$，有性质：

1. 使得 $\alpha_{n}\geq \limsup_{n\to \infty}\alpha_{n} + \varepsilon$ 成立的项至多有有限个。
2. 使得 $\alpha_{n}> \limsup_{n\to \infty}\alpha_{n}-\varepsilon$ 成立的项有无数个。
   $\limsup_{n\to \infty}\alpha_{n}$ 是数列 $\{\alpha_{n}\}$ 的最大极限点。

上下极限相等的充要条件是数列收敛

根据定理$1.3$ $\inf_{n>m}\alpha_{n}\leq\sup_{n>m}\alpha_{m}$ 所以 $\liminf_{n\to \infty} \alpha_{n}\leq \limsup_{ n \to \infty } \alpha_{n}$ ，其中等式成立的充分必要条件是数列 $\{\alpha_{n}\}$ 收敛。

Theorem 1.4.1
上下极限相等的充要条件是数列收敛

证明
$\implies$:，设 $\alpha=\liminf_{n\to \infty} \alpha_{n}= \limsup_{ n \to \infty } \alpha_{n}$
根据上下极限的性质，给定任意正实数$\varepsilon$，除了有限个项外 $\alpha-\varepsilon<\alpha_{n}<\alpha+\varepsilon$ 都成立。
由定理 $1.1$ 可知，此时$\{\alpha_{n}\}$ 收敛于 $\alpha$

$\impliedby$:，子列收敛于同一个极限。且根据定义 $\{\min\{\alpha_{m+n}\}\}$ 与 $\{\max\{\alpha_{m+n}\}\}$ 都是$\{\alpha_{n}\}$ 的子列，所以 $\alpha=\liminf_{n\to \infty} \alpha_{n}= \limsup_{ n \to \infty } \alpha_{n}$。

无穷级数

这一小节仅仅只是对无穷级数的简述。

Definition: 无穷级数
给定数列 $\{\alpha_{n}\}$ ，前 $n$ 项的部分和记为 $\sum^n_{k=1}\alpha_{k}$，$\sum^\infty_{n=1} \alpha_{n}$ 称为无穷级数。

Definition: 无穷级数的收敛
由部分$s_{n}=\sum^n_{k=1}\alpha_{k}$和构成的数列$\{s_{n}\}$ 收敛时，则称级数 $\sum^\infty_{n=1}\alpha_{n}$ 收敛。否则发散，由于$\{s_{n}\}$ 是单调非减的，所以只有肯呢个发散于正无穷 $\sum^\infty_{n=1}\alpha_{n}=+\infty$。

---

Theorem 1.5.1:
级数 $\sum^\infty_{n=1}|\alpha_{n}|$ 收敛，则 $\sum^\infty_{n=1}\alpha_{n}$ 也收敛

证明：
根据柯西收敛准则，给定任意正实数 $\varepsilon$ ，存在正整数 $n_{0}(\varepsilon)$ ，$n>m>n_{0}(\varepsilon)$ 时， $\left|\sum^n_{k=1}|\alpha_{k}|- \sum^m_{k=1}|\alpha_{k}| \right|=\left|\sum^n_{k=m+1}|\alpha_{k}|\right|\leq \varepsilon$

对于原级数， $\left|\sum^n_{k=1}\alpha_{k}- \sum^m_{k=1}\alpha_{k} \right|=|\sum^n_{k=m+1}\alpha_{k}|<\left|\sum^n_{k=m+1}|\alpha_{k}|\right|<\varepsilon$ ，满足柯西判别法，所以原级数 $\sum^\infty_{n=1}|\alpha_{n}|$ 也收敛。

当 $\sum^\infty_{n=1}|\alpha_{n}|$ 时收敛时，称 $\sum^\infty_{n=1}\alpha_{n}$ 绝对收敛。

---

Theorem 1.5.2
已知级数 $\sum^{\infty}_{n=1}r_{n}$ 收敛，且 $r_{n}\geq 0$， 对于级数 $\sum^\infty_{n=1} \alpha_{n}$ 如果存在正整数$m$，使得当 $n\geq m$时，$|\alpha_{n}|\leq r_{n}$ 成立，则 $\sum^\infty_{n=1} \alpha_{n}$ 绝对收敛。

由定理 1.5.1 易证：由于 $|\alpha_{n}|\leq r_{n}$ 所以 $\sum^n_{k=1}|\alpha_n|\leq \sum^n_{k=1}r_{n}$ ，根据定理1.5.1，由于 $\sum^n_{k=1}r_{n}$ 收敛，所以 $\sum^n_{k=1}|\alpha_n|$ 也收敛。

---

Theorem 1.5.3
数列 $\{\alpha_{n}\}$，$\alpha_{n}>0$，是收敛于 $0$ 的单调递减数列，则交错级数 $\sum^\infty_{n=1}(-1)^{n+1}\alpha_{n}$ 也收敛。

证明：
设 $s_{n} =\sum^n_{k=1}(-1)^{k+1}\alpha_{n}$ 则：

$\begin{aligned} s_{2n}=(a_{1}-a_{2})+(a_{3}-a_{4})+\dots+(a_{2n-1}-a_{2n}) \\ s_{2n-1}=a_{1}-(a_{2}-a_{3})-(a_{4}-a_{5})-\dots-(a_{2n-2}-a_{2n-1}) \end{aligned}$

且

$\begin{aligned} s_{1}>s_{3}>\dots>s_{2n-1}>\dots>s_{2n}>\dots>s_{4}>s_{2}\\ s_{2n-1}-s_{2n}=\alpha_{2n} \end{aligned}$

由于 $\alpha_{2n}\to 0$ ，给定 $m>n,q>n$，显然
$|s_{2m-1}-s_{2q-1}|<s_{2n-1}-s_{2n}=a_{2n}$
$|s_{2m}-s_{2q}|<s_{2n-1}-s_{2n}=a_{2n}$

由于 $\alpha_{2n}\to 0$ 根据柯西判别法，$\{s_{2n-1}\}$ 与 $\{s_{2n}\}$ 都收敛，也易得 $\lim_{ n \to \infty }s_{2n-1}=\lim_{ n \to \infty }s_{2n}$。由于 $\lim_{ n \to \infty }s_{2n-1}$与$\lim_{ n \to \infty }s_{2n-1}$ 实际上也是 $\{s_{n}\}$ 的上下极限，根据定理 1.4.1 可得$\{s_{n}\}$也收敛，设$\lim_{ n \to \infty }s_{n}=s$，此时任给正整数 $n$ 都有$s_{2n-1}<s<s_{2n}$