是一种寻找多元函数在一组约束下的极值的方法。通过引入拉格朗日乘子，将原问题的约束条件吸收进目标函数中形成新的函数，简化为无约束优化问题以方便求解：

  1. 构造拉格朗日函数 L(x,y,…,λ)=f(x,y,… )+λg(x,y,… )L(x,y,\dots,\lambda) = f(x,y,\dots) + \lambda g(x,y, \dots)，其中 f(x,y,… )f(x,y,\dots) 是原问题目标函数，g(x,y,… )g(x,y, \dots) 是约束条件。
  2. 求解方程组 ∂L∂x=0,∂L∂y=0,…,∂L∂λ=0\frac{ \partial L }{ \partial x }=0,\frac{ \partial L }{ \partial y }=0,\dots,\frac{ \partial L }{ \partial \lambda }=0，得到所有可能的极值点 (x,y,…,λ)(x,y,…,λ)。
  3. 将极值点代入目标函数 f(x,y,… )f(x,y,\dots)，比较大小，得到最大值和最小值。

假设要求 f(x,y)=x2+y2f(x,y) = x^2 + y^2 在约束条件 x+y=1x + y = 1 下的最小值。：

  1. 构造拉格朗日函数L(x,y,λ)=f(x,y)+λg(x,y)L(x,y,\lambda) = f(x,y) + \lambda g(x,y)，其中 g(x,y)=x+y−1g(x,y) = x + y - 1 是约束条件转换而来。
  2. 将偏导置零得到方程组 ∂L/∂x=2x+λ=0,∂L/∂y=2y+∂=0,∂/∂λL=x+y−1=0\partial L/\partial x = 2x + \lambda = 0,\partial L/\partial y = 2y + \partial = 0,\partial/\partial \lambda L = x + y - 1 = 0
  3. 解得  λ=−2,x=y=1/2\lambda = -2,x = y = 1/2，由于只有一组解，所以即为全局最优解。

对于不等式约束，需要通过 KKT 条件判断一个点是否是最优点。对于问题：

min⁡f(x)s.t.gi(x)≤0,i=1,…,mhj(x)=0,j=1,…,n\begin{aligned} \min \quad &f(x)\\ s.t. \quad &g_{i}(x)\leq 0,i=1,\dots,m\\ &h_{j}(x)=0,j=1,\dots,n \end{aligned}

可以构造一个拉格朗日函数：

L(x,λ,μ)=f(x)+∑i=1nλigi(x)+∑j=1nμjhj(x)L(x,\lambda,\mu)=f(x)+\sum_{i=1}^n\lambda_{i}g_{i}(x)+\sum_{j=1}^n\mu_{j}h_{j}(x)

对于一组解 x⋆,λ⋆,μ⋆x^\star,\lambda^\star,\mu^\star，使用KKT 条件判断是否是一个最优解：

  • 稳定性条件 ：∇L(x⋆,λ⋆,μ⋆)=0\nabla L(x^\star,\lambda^\star,\mu^\star)=0
  • 原始可行性：gi(x⋆)≤0;hj(x⋆)=0g_{i}(x^\star)\leq 0;h_{j}(x^\star)= 0
  • 对偶可行性：λi⋆≥0\lambda^\star_{i}\geq 0
  • 互补松弛可行性：λi⋆gi(x⋆)=0\lambda_{i}^\star g_{i}(x^\star)=0

知乎

对偶可行性


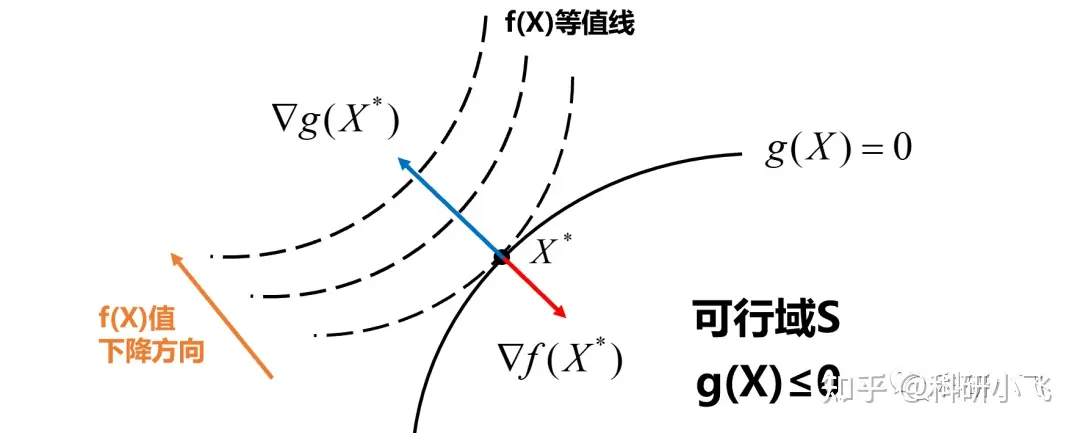
x⋆x^\star 若是一个最优解，在 x⋆x^\star 处，g(x)g(x) 与 f(x)f(x) 的梯度方向应该共线且相反，由稳定性条件可得
∇L(x⋆,λ⋆,μ⋆)=∇f(x⋆)+∑iλi∇gi(x⋆)=0  ⟹  λ∇g(x)=−∇f(x)\nabla L(x^\star,\lambda^\star,\mu^\star)=\nabla f(x^\star)+\sum_{i}\lambda_{i}\nabla g_{i}(x^{\star})=0\implies \lambda\nabla g(x)=-\nabla f(x)即λg(x)\lambda g(x)与f(x)f(x)梯度方向也相反，所以这里λ≥0\lambda\geq 0否则不满足g(x)g(x)与f(x)f(x)。

由于条件成立时，hj(x⋆)=0h_{j}(x^\star)=0，且gi(x⋆)≤0g_{i}(x^\star)\leq 0

f(x⋆)=g(λ⋆,μ⋆)≤f(x)+∑i=1nλi⋆gi(x⋆)+0f(x^\star)= g(\lambda^\star,\mu^\star)\leq f(x)+\sum_{i=1}^n\lambda_{i}^\star g_{i}(x^\star)+0

松弛互补可行性

x⋆x^\star 有 gi(x⋆)<0g_{i}(x^\star)< 0时，即正好满足约束，此时约束并不起作用，所以λi⋆=0\lambda_{i}^\star=0。
x∗x^* 有 gi(x⋆)=0g_{i}(x^\star)=0 时，即可以转换为等号约束条件。
而对于 g(x⋆)>0g(x^\star)>0的情况，不满足约束，需要舍弃。
在这两种满足约束的情况下λi⋆gi(x⋆)\lambda_{i}^\star g_{i}(x^\star)恒等 于00，即为松弛互补可行性。

拉格朗日对偶问题

把 L(x,λ,μ)L(x,\lambda,\mu) 看作是关于 λ,μ\lambda,\mu 的函数，求其最小值为拉格朗日对偶函数：

θ(x)=min⁡xL(x,λ,μ)\theta(x)=\min_{x} L(x,\lambda,\mu)

也可以表达为θ(x)=inf⁡x∈DL(x,λ,μ)\theta(x)=\inf_{x \in \mathbb{D}}L(x,\lambda,\mu)
则：

max⁡λ,μ;λ≥0θ(λ,μ)s.t.λ≥0\begin{aligned} \max_{\lambda,\mu;\lambda\geq 0} \quad &\theta(\lambda,\mu)\\ s.t. \quad &\lambda\geq 0 \end{aligned}

称为原问题的拉格朗日对偶问题，常通过对xx求导并置零来获得对偶函数的表达形式（KKT的稳定性条件）。

若

max⁡λ,μ;λ≥0θ(λ,μ)≤min⁡xmax⁡λ,μ;λ≥0L(x,λ,μ)\max_{\lambda,\mu;\lambda\geq 0}\theta(\lambda,\mu)\leq \min_{x} \max_{\lambda,\mu;\lambda\geq 0}L(x,\lambda,\mu)

则称为弱对偶，若

max⁡λ,μ;λ≥0θ(λ,μ)=min⁡xmax⁡λ,μ;λ≥0L(x,λ,μ)\max_{\lambda,\mu;\lambda\geq 0}\theta(\lambda,\mu)= \min_{x} \max_{\lambda,\mu;\lambda\geq 0}L(x,\lambda,\mu)

称为强对偶。

无论原问题是否为凸，对偶问题总是凸的，因为是关于λ\lambda和μ\mu的仿射函数。