数学分析 - 连续函数
Definition 连续函数
设 f(x)f(x)f(x) 是区间 U∘(x0)U^\circ(x_{0})U∘(x0) 处有定义的函数,若
limx→x0f(x)=f(x0)\lim_{ x \to x_{0} } f(x)=f(x_{0})
x→x0limf(x)=f(x0)
则称 f(x)f(x)f(x) 在 x0x_{0}x0 处连续。
若在其定义域上每一点都连续,则称 f(x)f(x)f(x) 为连续函数。
若 limx→x0+f(x)=f(x0)\lim_{ x \to x_{0}^+ }f(x)=f(x_{0})limx→x0+f(x)=f(x0) / limx→x0−f(x)=f(x0)\lim_{ x \to x_{0}^- }f(x)=f(x_{0})limx→x0−f(x)=f(x0) 则称 f(x)f(x)f(x) 在 x0x_{0}x0 处 右/左 连续。
若在区间 III 上每一点都连续称 f(x)f(x)f(x) 在 III 上连续。对于半开半闭与闭区间上定义的函数,只在这些点上考虑左连续/右连续
Definitio ...
数学分析 - 函数极限
Definition: 函数 f(x)f(x)f(x)
对集合 DDD 中的每个元素 xxx 都对应有一个yyy,则称这对应关系是由 DDD 定义的函数,xxx 对应的值记为 f(x)f(x)f(x),DDD 是函数的定义域,全体值的集合 {f(x)∣x∈D}\{ f(x)| x \in D\}{f(x)∣x∈D} 称为函数 fff 的值域。
类似数列的极限的定义,我们同样使用 ε\varepsilonε-nnn 语言描述,但是函数的收敛我们讨论的更复杂一些,数列仅讨论 n→∞n\to \inftyn→∞ 时 ana_{n}an 的敛散,而函数不仅要讨论 x→+∞x\to +\inftyx→+∞ 时的极限,还有 x→−∞x\to -\inftyx→−∞、x→∞x\to \inftyx→∞、x→x0x\to x_{0}x→x0
Definition: 函数 x→+∞x\to +\inftyx→+∞ 时的极限
∀ε>0,∃v(ε)\forall \varepsilon>0,\exists v(\varepsilon)∀ε>0,∃v(ε),使得x>v(ε) ...
数学分析 - 平面
1. 基本概念
直积集合 R×R\mathbb{R}\times \mathbb{R}R×R 称为平面,用 R2\mathbb{R}^2R2 简化表示,元素 (x,y)∈R2(x,y) \in \mathbb{R}^2(x,y)∈R2 称为平面上的点。
点 P=(x,y)P=(x,y)P=(x,y),Q=(u,v)Q=(u,v)Q=(u,v) ,点 PPP 与 QQQ 的距离定义为:
∣PQ∣=(x−u)2+(y−v)2|PQ|=\sqrt{(x-u)^2+(y-v)^2}
∣PQ∣=(x−u)2+(y−v)2
当 P≠QP\neq QP=Q 时,PPP 与 QQQ 连接而成的线段 PQPQPQ 定义为线段上点的全体集合:
PQ={(λx+(1−λ)u,λy+(1−λ)u)∣λ∈[0,1]}PQ=\{(\lambda x+(1-\lambda) u,\lambda y+(1-\lambda) u)|\lambda \in[0,1]\}
PQ={(λx+(1−λ)u,λy+(1−λ)u)∣λ∈[0,1]}
过 PPP 、QQQ 的直线定义为:
lPQ={(λx+(1−λ)u,λy+ ...
数学分析 - 数列
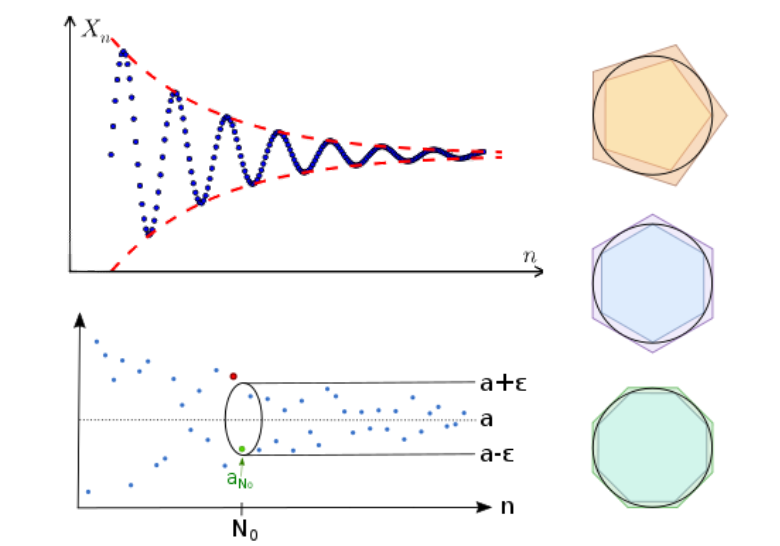
数列极限的定义
数列:α1,α2,…,αn,…\alpha_{1},\alpha_{2},\dots,\alpha_{n},\dotsα1,α2,…,αn,…这样排成一列的实数称为数列。
如果 ana_{n}an 随着 nnn 充分增大,逐渐接近为一个实数 α\alphaα 时,称,数列 {αn}\{\alpha_{n}\}{αn} 收敛于α\alphaα。
但是,“充分增大”,“逐渐接近”这些词是模糊不清,缺乏严谨的,应该避免使用。
很容易知道,如果 {αn}\{\alpha_{n}\}{αn} 收敛于 α\alphaα,说明,随着 nnn 的增大,αn\alpha_{n}αn 与 α\alphaα 的距离会越来越小,即,无论我们取多么小的一个距离 ε\varepsilonε,随着 nnn 的增大,某一项 n0(ε)n_{0}(\varepsilon)n0(ε) (可以由 ε\varepsilonε 决定,是一个关于 ε\varepsilonε 的表达式)之后,αn\alpha_{n}αn 与 α\alphaα,之间的距离总会比这个距离还小。
这样的表述很好的避免使 ...
EnsembleLearning
多个学习器被训练来解决同一个问题。往往比单个学习器好很多。
一般结构为:先产生一组“个体学习器”,再用某种策略将它们结合起来。集成学习大致可分为三大类:
Bagging(Bootstrap Aggregating):有放回的抽样原始数据集,分别训练多个学习器,将多个模型的输出加权平均作为最终结果。e.g. 随机森林
Boosting:通过在训练新模型实例时更注重先前模型错误分类的实例来增量构建集成模型。e.g. AdaBoost GBDT
Stacking:训练一个模型用于组合其他各个模型。
Bagging
随机森林
给定
数据集 D∈RND\in R^ND∈RN
树数量 MMM,树数量越多,泛化能力越强,但是过大训练速度慢提升也很小。
每棵树所能使用的最大特征数 kkk
算法过程:
循环训练MMM个决策树,{Tm}m=1M\{T_{m}\}^M_{m=1}{Tm}m=1M
从数据集 D∈RND\in R^ND∈RN 随机选取kkk个特征得到的子集 Dm′∈RND^\prime_{m} \in R^NDm′∈RN (显然数据集中可能会有重复的样本)
使用Dm′D^\p ...
聚类
一种无监督学习方法,通过无标签的训练样本,学习数据潜在规律,将数据集中的样本划分为多个不相交的子集(簇 cluster),每个子集可能会对应一个潜在的概念,为进一步数据分析提供基础。
聚类是个模糊且庞大的算法,几个常见的聚类模型:
质心聚类(原型聚类):每个聚类由一个中心向量表示,可以不属于数据集。
密度聚类:聚类被定义为密度高于数据集其余部分的区域,稀疏区域中的对象通常被认为是噪声和边界点。
分布模型聚类:被定义为最有可能属于同一分布的对象。这种方法可以捕获属性之间的相关性和依赖性,但对于许多真实数据集,可能没有简明定义的数学模型.
连通性聚类:根据一个样本附近样本的相似性,将他们连接起来,所有连在一起的样本被认为是一个簇
算法
k-means
是一种质心聚类。给定数据集DDD,需要kkk个原型(均值向量)μ={μ1,…,μk}\mu=\{\mu_{1},\dots,\mu_{k}\}μ={μ1,…,μk},来划分为 kkk 个簇C={C1,…Ck}C=\{C_{1},\dots C_{k}\}C={C1,…Ck}。
目标是:minμ∑in∑x∈Ci∣∣x−μj∣∣2\ ...
最优化 - 二次规划
目标函数是变量的二次函数,约束条件是变量的线性不等式:
minx12xTQx+cTxs.t.Ax≤b\begin{aligned}
\min_{x} \quad &\frac{1}{2} x^T Q x + c^T x \\
s.t.\quad &Ax \leq b
\end{aligned}
xmins.t.21xTQx+cTxAx≤b
其中,x∈Rn,c∈Rn,b∈Rn,A∈Rm×nx\in\mathbb{R}^n,c\in\mathbb{R}^n,b\in\mathbb{R}^n,A\in\mathbb{R}^{m \times n}x∈Rn,c∈Rn,b∈Rn,A∈Rm×n,Q∈Rn×nQ\in\mathbb{R}^{n \times n}Q∈Rn×n是一个对称矩阵。
例如:x=[x1,x2]Tx=[x_{1},x_{2}]^Tx=[x1,x2]T,Q=(a1a2a2a3)Q=\left(\begin{matrix}a_{1} \quad a_{2}\\a_{2} \quad a_{3}\end{matrix}\right)Q=(a1a2a2 ...
最优化 - 拉格朗日乘子法
是一种寻找多元函数在一组约束下的极值的方法。通过引入拉格朗日乘子,将原问题的约束条件吸收进目标函数中形成新的函数,简化为无约束优化问题以方便求解:
构造拉格朗日函数 L(x,y,…,λ)=f(x,y,… )+λg(x,y,… )L(x,y,\dots,\lambda) = f(x,y,\dots) + \lambda g(x,y, \dots)L(x,y,…,λ)=f(x,y,…)+λg(x,y,…),其中 f(x,y,… )f(x,y,\dots)f(x,y,…) 是原问题目标函数,g(x,y,… )g(x,y, \dots)g(x,y,…) 是约束条件。
求解方程组 ∂L∂x=0,∂L∂y=0,…,∂L∂λ=0\frac{ \partial L }{ \partial x }=0,\frac{ \partial L }{ \partial y }=0,\dots,\frac{ \partial L }{ \partial \lambda }=0∂x∂L=0,∂y∂L=0,…,∂λ∂L=0,得到所有可能的极值点 (x,y,…,λ)(x,y,…,λ)(x,y,…,λ)。
将极值 ...
支持向量机
是一种二分类模型,目的是找到一个超平面,使得它能够正确划分训练数据集,并且使得训练数据集中离超平面最近的点(即支持向量)到超平面的距离最大。
硬间隔SVM
定义有三个超平面:
超平面: wTx+b=0w^Tx+b=0wTx+b=0,这个超平面用于在预测时,判断在两个超平面之间的样本点。
正超平面:wTx+b=1w^Tx+b=1wTx+b=1,优化时,保证正类都在其之上
负超平面:wTx+b=−1w^Tx+b=-1wTx+b=−1,优化时,保证负类都在其之下
样本中任意点到超平面wTx+b=0w^Tx+b=0wTx+b=0的距离可以写为:
ri=∣wTx+b∣∥w∥r_{i}=\frac{|w^Tx+b|}{\Vert w \Vert }
ri=∥w∥∣wTx+b∣
假设正超平面到超平面的距离为 r+r^+r+
{wTx+b=1∣wTx+b∣∥w∥=r+\begin{cases}
w^Tx+b=1 \\
\frac{|w^Tx+b|}{\Vert w\Vert }=r^+
\end{cases}
{wTx+b=1∥w∥∣wTx+b∣=r+
解得
r+=1∥w∥r^+=\f ...
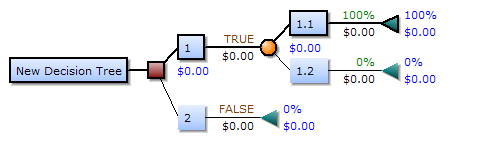
决策树
用一棵树来表示数据的分类或回归规则。每个节点表示一个属性的判别,每个分支表示判别的结果,每个叶节点表示一个类别或一个数值。决策树的生成过程是不断地选择最优的属性来划分数据集,使得每个子集的纯度越来越高。
或者说,决策树是在不断的按照某个属性,把训练样本细分为多个子集,直到已经只含有某一类的样本。
决策树的纯度可以用信息熵或基尼系数等指标来度量,它们反映了数据集合中不同类别的混乱程度。
选择最优的划分属性
随着不断划分,我们希望决策树的结点纯度越来越高。
信息熵 Information Entropy
信息熵,可以表征随机变量分布的混乱程度,某个事件发生不确定度越大,熵越大,随机变量 XXX 中 iii 事件发生可能性为 pip_ipi,(或者说,样本集 XXX 中 iii 类样本所占比例为 pip_ipi),信息熵定义为:
Ent(X)=−∑i=1Npilog2piEnt(X)=-\sum^N_{i=1}p_i \log_2 p_i
Ent(X)=−i=1∑Npilog2pi
熵的计算只与事件概率有关,与值无关,且约定p=0p=0p=0时plogp=0p \log p= ...