是一种二分类模型，目的是找到一个超平面，使得它能够正确划分训练数据集，并且使得训练数据集中离超平面最近的点（即支持向量）到超平面的距离最大。

硬间隔SVM

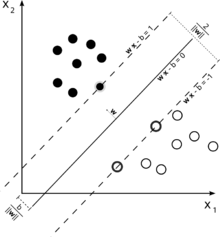
定义有三个超平面：

  1. 超平面： wTx+b=0w^Tx+b=0，这个超平面用于在预测时，判断在两个超平面之间的样本点。
  2. 正超平面：wTx+b=1w^Tx+b=1，优化时，保证正类都在其之上
  3. 负超平面：wTx+b=−1w^Tx+b=-1，优化时，保证负类都在其之下

样本中任意点到超平面wTx+b=0w^Tx+b=0的距离可以写为：

ri=∣wTx+b∣∥w∥r_{i}=\frac{|w^Tx+b|}{\Vert w \Vert }

假设正超平面到超平面的距离为 r+r^+

{wTx+b=1∣wTx+b∣∥w∥=r+\begin{cases} w^Tx+b=1 \\ \frac{|w^Tx+b|}{\Vert w\Vert }=r^+ \end{cases}

解得

r+=1∥w∥r^+=\frac{1}{\Vert w\Vert }

在我们的定义中正负两超平面对称，r+=r−r^+=r^-，即正负超平面之间的间隔 r=2r+r=2r^+：

r=2∥w∥(1)r=\frac{2}{\Vert w\Vert }\tag{1}

此时若能正确分类则任意的样本点(x(i),y(i))(x^{(i)},y^{(i)})满足：

{wTx(i)+b≥1,yi=1wTx(i)+b≤−1,yi=−1\begin{cases} w^Tx^{(i)}+b\geq 1&,y^{i}=1 \\ w^Tx^{(i)}+b\leq -1&,y^{i}=-1 \end{cases}

由于，标签y(i)∈(+1,−1)y^{(i)} \in(+1,-1)，如果模型预测正确，则预测值的符号与标签符号相等，积大于11
所以可以将上式简写为：

y(i)(wTx(i)+b)≥1(2)y^{(i)}(w^Tx^{(i)}+b)\geq 1 \tag{2}

为了模型的泛化性能，我们希望，间隔 rr 越大越好：

max⁡w,br=min⁡w,b1r=min⁡w,b12∥w∥=min⁡w,b12∥w∥2=min⁡w,b12wTw\begin{aligned} \max_{w,b} r &= \min_{w,b} \frac{1}{r}\\ &=\min_{w,b} \frac{1}{2}\Vert w\Vert \\ &=\min_{w,b} \frac{1}{2}\Vert w\Vert ^2\\ &=\min_{w,b} \frac{1}{2}w^Tw \end{aligned}

此时优化目标可以描述为一个凸二次规划问题

min⁡w,b∥w∥2s.t.  ∀i   y(i)(wTx(i)+b)≥1  and  ζi≥0(3)\begin{aligned} &\min_{w,b} \Vert w\Vert ^2\\ &s.t. \ \ \forall i \ \ \ y^{(i)}(w^Tx^{(i)}+b)\geq 1 \ \ \text{and} \ \ \zeta_{i}\geq 0 \end{aligned}\tag{3}

注意，硬间隔无法解决线性不可分的问题，因此，需要迎入软间隔。

软间隔

很多情况下，数据是线性不可分的，即，永远无法满足式(2)(2)，此时我们需要引入铰链损失：

ζi=max⁡(0,1−y(i)(wTx(i)+b))(4)\zeta_{i}=\max(0,1-y^{(i)}(w^Tx^{(i)}+b)) \tag{4}

即，若样本点 x(i)x^{(i)} 被正确分类时，损失为 00，被错误分类时，损失的值与到超平面（并非正超平面或负超平面）的距离成正比。

对于目标(1)(1)改为：

λ∑iζi+12∥w∥2\lambda\sum_{i}\zeta_{i}+\frac{1}{2}\Vert w\Vert ^2

对于条件(2)(2)改为：

y(i)(wTx(i)+b)≥1−ζi(5)y^{(i)}(w^Tx^{(i)}+b)\geq 1 -\zeta_{i} \tag{5}

即，对于被错误分类的样本点，不进行约束。
原问题改为：

min⁡w,b12∥w∥2+λ1n∑iζis.t.  ∀i  −y(i)(wTx(i)+b)−1+ζi≤0  and  −ζi≤0(6)\begin{aligned} &\min_{w,b} \frac{1}{2}\Vert w\Vert ^2+\lambda\frac{1}{n}\sum_{i}\zeta_{i}\\ &s.t. \ \ \forall i\ \ -y^{(i)}(w^Tx^{(i)}+b)-1+\zeta_{i}\leq0 \ \ \text{and} \ \ -\zeta_{i}\leq 0 \\ \end{aligned}\tag{6}

λ\lambda 表示了间隔大小的重要程度，仍然是凸优化问题强对偶性成立，其拉格朗日函数为：

L(w,b,α,μ)=12∥w∥2+λ∑iζi−∑iαi[y(i)(wTx(i)+b)−1+ζi]−∑iμiζiL(w,b,\alpha,\mu)=\frac{1}{2}\Vert w\Vert ^2+\lambda\sum_{i}\zeta_{i}-\sum_{i}\alpha_{i}\left[y^{(i)}(w^Tx^{(i)}+b)-1+\zeta_{i}\right]-\sum_{i}\mu_{i}\zeta_{i}

分别对w,bw,b求偏导并置00，由于这里对 ζ\zeta 求导比较复杂，可以直接LL对 ζ\zeta 求导，因为

f(x,y)=g(x,y,h(x,y))f(x,y)=g(x,y,h(x,y))

∂f∂x=∂f∂h∂h∂x\frac{\partial f}{\partial x}=\frac{\partial f}{\partial h}\frac{\partial h}{\partial x}

若导数存在且 ∂f∂h∣h=h⋆=0\frac{\partial f}{\partial h}|_{h=h^\star}=0，必然 ∂f∂x∣h=h⋆=0\frac{\partial f}{\partial x}|_{h=h^\star}=0，意义相同。

所以拉格朗日函数对w,b,ζw,b,\zeta分别求偏导得到：

∂L∂w=w−∑iαiy(i)x(i)=0  ⟹  w=∑iαiy(i)x(i)∂L∂b=∑iαiy(i)=0∂L∂ζ=λ−α−μ=0  ⟹  λ−μ=α(7)\begin{aligned} \frac{ \partial L }{ \partial w } &=w-\sum_{i}\alpha_{i} y^{(i)}x^{(i)}=0 \implies w=\sum_{i}\alpha_{i}y^{(i)}x^{(i)} \\ \frac{ \partial L }{ \partial b } &= \sum_{i}\alpha_{i} y^{(i)}=0\\ \frac{ \partial L }{ \partial \zeta } &=\lambda- \alpha-\mu=0 \implies \lambda-\mu=\alpha \end{aligned}\tag{7}

其中1∈Rn,∀i  1i=1\mathbb{1}\in \mathbb{R}^n,\forall i \ \ \mathbb{1}_{i}=1，α={αi}i=1n\alpha=\{\alpha_{i}\}^n_{i=1}，μ={μi}i=1n\mu=\{\mu_{i}\}^n_{i=1}

代回拉格朗日函数，得到拉格朗日对偶函数：

g(α,μ)=12wTw−wT∑iαiy(i)x(i)+∑iαiy(i)b+∑iαi+λ∑iζi−∑iαiζi−∑iμiζig(α,μ)=wT(w−αiy(i)x(i))−12wTw+b∑iαiy(i)+∑iαi+∑(λ−α−μ)ζg(α,μ)=−12wTw+∑iαi+∑(λ−α−μ)ζg(α,μ)=−12∑i∑jαiy(i)(x(i)Tx(j))αjy(j)+∑iαi\begin{aligned} g(\alpha,\mu)&=\frac{1}{2} w^Tw-w^T\sum_{i}\alpha_{i}y^{(i)}x^{(i)}+\sum_{i}\alpha_{i}y^{(i)}b+\sum_{i}\alpha_{i}+\lambda\sum_{i}\zeta_{i}-\sum_{i}\alpha_{i}\zeta_{i}-\sum_{i}\mu_{i}\zeta_{i}\\ g(\alpha,\mu)&=w^T(w-\alpha_{i}y^{(i)}x^{(i)})-\frac{1}{2}w^Tw+b\sum_{i}\alpha_{i}y^{(i)}+\sum_{i}\alpha_{i}+\sum \left( \lambda-\alpha-\mu \right)\zeta\\ g(\alpha,\mu)&=-\frac{1}{2}w^Tw+\sum_{i}\alpha_{i}+\sum \left( \lambda-\alpha-\mu \right)\zeta\\ g(\alpha,\mu)&=-\frac{1}{2}\sum_{i}\sum_{j}\alpha_{i}y^{(i)}({x^{(i)}}^Tx^{(j)})\alpha_{j}y^{(j)}+\sum_{i}\alpha_{i} \end{aligned}

由于松弛互补可行性，需要满足：$$a_{i}y^{(i)}=0$$
由于式(7.2)(7.2)与(7.3)(7.3)：

λ−α=μ≥0α≤λ\begin{aligned} \lambda-\alpha=\mu\geq 0\\ \alpha\leq \lambda \end{aligned}

并与对偶可行性融合：

0≤α≤λ0\leq \alpha\leq \lambda

则简化后的对偶问题表述为：

max⁡w,b−12∑i∑jαiy(i)(x(i)Tx(j))αjy(j)+∑iαis.t.  ∀i  αiy(i)=0  and  0≤αi≤λ\begin{aligned} &\max_{w,b} -\frac{1}{2}\sum_{i}\sum_{j}\alpha_{i}y^{(i)}({x^{(i)}}^Tx^{(j)})\alpha_{j}y^{(j)}+\sum_{i}\alpha_{i}\\ &s.t. \ \ \forall i\ \ \alpha_{i}y^{(i)}=0 \ \ \text{and} \ \ 0\leq \alpha_{i}\leq \lambda \end{aligned}

转为最小化，并转为二次规划的一般形式：

max⁡w,bg(α,μ)=min⁡w,b12∑i∑jαiy(i)(x(i)Tx(j))αjy(j)−∑iαi\max_{w,b} g(\alpha,\mu)=\min_{w,b}\frac{1}{2}\sum_{i}\sum_{j}\alpha_{i}y^{(i)}({x^{(i)}}^Tx^{(j)})\alpha_{j}y^{(j)}-\sum_{i}\alpha_{i}

令Q={Qi,j}i=1,j=1nQ=\{Q_{i,j}\}_{i=1,j=1}^n，原问题可描述为：

min⁡w,b12αTQα−1Tαs.t.  αTy=0  and  0≤α≤λ(8)\begin{aligned} &\min_{w,b}\frac{1}{2}\alpha^TQ\alpha-\mathbb{1}^T\alpha \\ &s.t. \ \ \alpha^Ty=0 \ \ \text{and} \ \ 0\leq \alpha\leq \lambda \end{aligned}\tag{8}

以方便的使用二次规划算法解出，对于最优解α⋆\alpha^\star，原问题最优解：

w⋆=∑iαi⋆y(i)x(i)w^\star=\sum_{i}\alpha^\star_{i}y^{(i)}x^{(i)}

y(i)(wTx(i)+b)=1⟺b=1y(i)−wTx(i)y^{(i)}(w^Tx^{(i)}+b)=1\Longleftrightarrow b=\frac{1}{y^{(i)}}- w^Tx^{(i)}

由于y(i)∈+1,−1y^{(i)}\in{+1,-1}，1y(i)=y(i)\frac{1}{y^{(i)}}=y^{(i)}

b⋆=1yi−w⋆Tx(i)b^\star=\frac{1}{y^{i}}-{w^\star}^Tx^{(i)}

核方法

与线性回归的激活函数类似，通过一个非线性函数ϕ(⋅)\phi(\cdot)来映射数据使得更容易线性可分。对于核函数的选择，是SVMSVM最重要的问题，直接决定了是否能有效分类。
对称函数K(x(i),x(j))=ϕ(x(i))Tϕ(x(j))\mathcal{K}(x^{(i)},x^{(j)})=\phi(x^{(i)})^T\phi(x^{(j)})
对于数据集D={x(1),…,x(n)}D=\{x^{(1)},\dots,x^{(n)}\}，K\mathcal{K}的核矩阵：

K=[K(x1,x1) … K(x1,xn)…K(xn,x1) …K(xn,xn]K=\left[\begin{matrix} \mathcal{K}(x_{1},x_{1}) \ \dots \ \mathcal{K}(x_{1},x_{n}) \\ \dots \\ \mathcal{K}(x_{n},x_{1}) \ \dots \mathcal{K}(x_{n},x_{n} \end{matrix}\right]

是半正定的，则这个函数就能作为核函数使用，此时目标可以写为：

min⁡w,b12∑i∑jαiy(i)K(xi,xj)αjy(j)−∑iαi\min_{w,b}\frac{1}{2}\sum_{i}\sum_{j}\alpha_{i}y^{(i)}\mathcal{K}(x_{i},x_{j})\alpha_{j}y^{(j)}-\sum_{i}\alpha_{i}

常见核函数：

  • 线性核：x(i)Tx(j){x^{(i)}}^Tx^{(j)}
  • 多项式核：(x(i)Tx(j))({x^{(i)}}^Tx^{(j)})
  • 高斯核：exp⁡(−∥x(i)−x(j)∥22σ2)\exp \left(-\frac{\Vert x^{(i)}-x^{(j)}\Vert^2 }{2\sigma^2}\right)
  • 拉普拉斯核：exp⁡(−∥x(i)−x(j)∥2σ)\exp\left( -\frac{\Vert x^{(i)}-x^{(j)}\Vert }{2\sigma} \right)
  • Sigmoid 核：tanh⁡(βx(i)Tx(j)+θ)\tanh(\beta {x^{(i)}}^Tx^{(j)}+\theta)