决策树

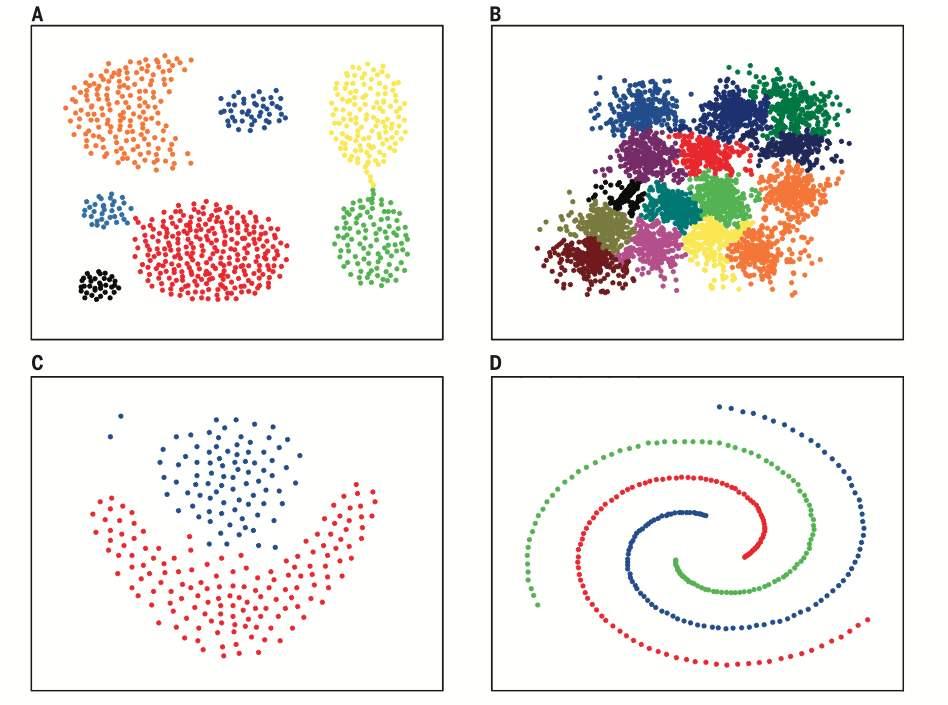
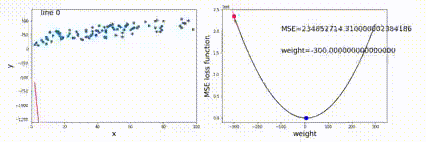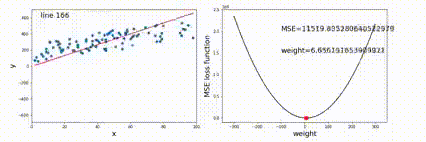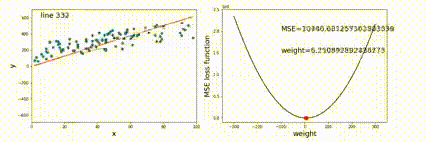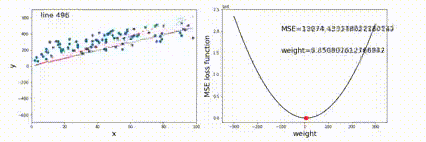
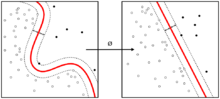
用一棵树来表示数据的分类或回归规则。每个节点表示一个属性的判别，每个分支表示判别的结果，每个叶节点表示一个类别或一个数值。决策树的生成过程是不断地选择最优的属性来划分数据集，使得每个子集的纯度越来越高。

或者说，决策树是在不断的按照某个属性，把训练样本细分为多个子集，直到已经只含有某一类的样本。

决策树的纯度可以用信息熵或基尼系数等指标来度量，它们反映了数据集合中不同类别的混乱程度。

选择最优的划分属性

随着不断划分，我们希望决策树的结点纯度越来越高。

信息熵 Information Entropy

信息熵，可以表征随机变量分布的混乱程度，某个事件发生不确定度越大，熵越大，随机变量 $X$ 中 $i$ 事件发生可能性为 $p_i$，（或者说，样本集 $X$ 中 $i$ 类样本所占比例为 $p_i$），信息熵定义为：

$Ent(X)=-\sum^N_{i=1}p_i \log_2 p_i$

熵的计算只与事件概率有关，与值无关，且约定$p=0$时$p \log p=0$

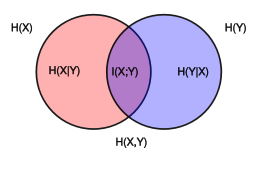
条件信息熵，已知$X$的条件下随机变量$Y$的不确定性。

$\begin{aligned} Ent(Y|X)&=-\sum_{x \in X}P(x) Ent(Y|X=x)\\ &= -\sum_{x \in X}P(x)\sum_{y \in Y}P(y|x)\log p(y|x)\\ &= -\sum_{x \in X,y \in Y}P(x,y)\log P(y|x)\\ &= \sum_{x \in X,y \in Y}P(x,y)\log \frac{p(x)}{p(x,y)} \end{aligned}$

联合信息熵：

$Ent(X,Y)=Ent(X,Y)-Ent(X)$

互信息度量了两个变量之间相互依赖的程度

$I(X;Y)=\sum_{y \in Y,x \in X}p(x,y)\log\left( \frac{p(x,y)}{p(x)p(y)} \right)$

信息增益表示在一个条件下，信息不确定性减少的程度（按某个特征划分数据集获得的增益）：

$Gain(X,Y)=H(Y)-H(Y|X)$

信息增益越大，意味着使用属性$Y$来进行划分所得的纯度提升越大，以此来选择最优划分属性。

若将数据序号这类作为条件，则不会有任何不确定性，但是这个条件是没有意义的，信息增益率在信息增益的基础上增加了惩罚项。

$GainRate(X,Y)=\frac{Gain(X,Y)}{H(Y)}$

基尼系数（基尼不纯度）

与信息熵一样表征事件不确定性， 或者说，从数据集中随机抽取两个样本，其类别不一致的概率

$\begin{aligned} Gini(X)&= \sum_{x \in X}P(x)(1-P(x))\\ &=1-\sum_{x \in X}P(x)^2 \end{aligned}$

对于数据集$Y$,根据特征$X$的某个值$x$把$Y$分成$Y|X=x$与$Y|X\neq x$，此时条件基尼系数：

$Gini(Y|X=x)=P(Y|X=x)Gini(Y|X=x)+(1-P(Y|X=x))Gini(Y|X\neq x)$

基尼系数也可以视为信息熵的近似，信息熵的泰勒展开第一项就是基尼指数。

剪枝 Pruning

是一种防止过拟合的方法，它可以通过删除不必要的子树或节点来降低决策树的复杂度，提高泛化能力。

• 预剪枝是在生成决策树的过程中，根据一些条件（如最小节点样本数、最大深度、信息增益、精度等）来判断是否继续划分
• 后剪枝是在生成完整的决策树后，从下往上检查每个子树是否对模型有贡献，如果没有或很小，就将其替换为叶节点或删除。

算法

ID3

ID3（Iterative Dichotomiser 3），是处理离散数据的决策树算法，可以归纳为以下几点：

1. 使用所有没有使用的属性并计算与之相关的样本熵值]
2. 选取其中熵值最小的属性
3. 生成包含该属性的节点
   python 伪代码，完整代码

dataset: list[list]  # 数据集 e.g. [feature1,feature2,...,class]labels: list[str]  # feature对应的特征名  
  
def info_ent(dataset: list) -> float: ...  # 计算集合dataset的信息熵  
def cond_info_ent(dataset: list, feature_id: list)->float:...  # 计算feature_id下的条件熵  
 
 
def split_set(dataset, label_id, value):  
    new_dataset = []  
    for sample in dataset:  
        if sample[label_id] == value:  
            # 去掉已经遍历过的特征，并加进新集合  
            new_dataset.append(list(sample)[:label_id] + list(sample)[label_id + 1:])  
    return np.array(new_dataset)
  
  
def get_best_feature_label(dataset, labels) -> str:  
    # 选择最好的划分特征的label  
    ent = info_ent(dataset)  
    gains = []  
    for i in range(len(labels)):  
        # 计算按 feature=i 划分下的条件熵，并计算信息增益  
        cond_ent = cond_info_ent(dataset, i)  
        gain = ent - cond_ent  
        gains.append(gain)  
    best_feature = gains.index(max(gains))  
    return labels[best_feature]
  
  
def create_tree(dataset, labels):  
    # 所有类别  
    classes = dataset[:, -1]  
    if len(set(classes)) == 1:  
        # 如果集合内所有元素类别相同，终止递归，返回类别  
        return classes[0]  
    if len(labels) == 0:  
        # 所有特征都遍历完了，则返回出现次数最多的类别  
        return max(list(classes), key=list(classes).count)  
    best_label = get_best_feature_label(dataset, labels)  
    best_label_id = labels.index(best_label)  
    tree = {best_label: {}}  
    # 删除已经访问过的特征  
    del labels[best_label_id]  
    feature_value = set([sample[best_label_id] for sample in dataset])  
    for value in feature_value:  
        tree[best_label][value] = create_tree(split_set(dataset, best_label_id, value), labels)  
    return tree
  
  
create_tree(dataset, labels)

缺陷：

• 没有剪枝等操作，容易过拟合
• 无法处理带有缺失值的数据
• 信息增益计算方式会倾向选择特征选项较多的属性
• 类别不平衡会导致效果很差

变体：

• C4.5：改为使用信息增益率来选择属性，在树构造过程中进行悲观剪枝，对不完整数据进行处理（以不同概率划分到不同节点），讲连续属性离散化。
• CART：可以做回归任务，使用gini系数选择属性，采用代理测试估计缺失值，使用代价复杂性剪枝，对类别进行加权减少类别不平衡带来的影响，与 ID3 和 C4.5 的多叉树不同，CART是二叉树，CART 可多次重复使用特征。

CART

回归树

给定划分$D^+,D^-$，为了使得这个划分出的集合的值与标签误差最小，划分后节点的值显然应该是集合的平均值，$c_{i}=avg(y_{i}|x_i \in D)$。

对于选择哪个属性与分割方式，我们其最小化均方误差

$E = \sum_{x_{i \in D^+}}(y_{i}-c_{i})^2+\sum_{x_{i \in D^-}}(y_{i}-c_{i})^2$

由于给定划分时，$c_{i}$我们通过取平均已知，所以只需要遍历所有可能的划分，取均方误差最小的划分方式即可。

分类树

分类树用基尼指数选择最优特征。

$\begin{aligned} Gini(X)&= \sum_{x \in X}P(x)(1-P(x))\\ &=1-\sum_{x \in X}P(x)^2 \end{aligned}$

具体处理与ID3算法类似

离散属性的划分

对离散属性选取一个值，进行二元分割为等于这个值的与不等于这个值的，{A,B,C} -> {A},{B,C} 或 {B},{A,C} 或 {C},{A,B}

连续属性的划分

对连续属性取属性相邻值的平均值作为间断点，二元分类，{1,2,5}，$\varepsilon=1.5$ 或$\varepsilon=3.5$ -> {1},{2,5} 或 {1,2},{5}

剪枝操作

• 预剪枝：
  • 当分割后的样本个数小于预定阈值
  • 对于连续属性的划分，若其最终均方误差$E$的减小幅度小于预定阈值，则停止划分
• 后剪枝：树建立完成后，使用测试集自上而下判断节点划分是否能够降低误差，如果不能则合并这些节点。