xt+1:=xt−η∇f(xt)
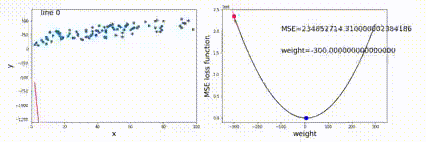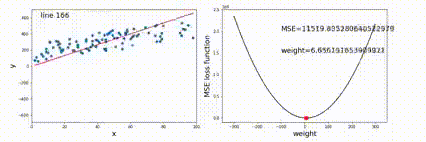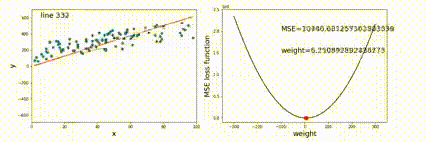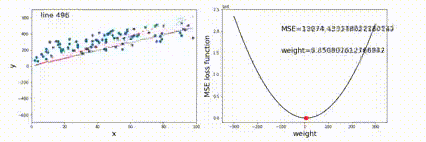
为了让 f(x) 的值越来越小,需要不断迭代优化 x 的值,x 优化是方向是 f 的梯度的反方向,快慢受到学习率 η 的影响。
梯度下降的本质
梯度下降的本质是,将目标函数 f(x) 近似为其在某点 xt 处的一阶泰勒展开,记为 fˉ(x;xt) :
f(x)≈fˉ(x;xt)=f(xt)+f′(xt)(x−xt)
注意,只有在 xt→x 时误差 f(x)−fˉ(x;xt) 才趋近于 0,所以,我们要在 xt 附近找一点 xt+1=xt+Δ ,代入 fˉ 可得:
fˉ(xt+Δ;xt)=f(xt)−f′(xt)⋅Δ
我们希望,f(xt+1)<f(xt) ,也就是 fˉ(xt+1;xt)<f(xt) ,观察上式可以发现,只要令 f′(xt)⋅Δ<0 就能保证 fˉ(xt+1;xt)<f(xt) 。
其中 Δ 是可以由我们自由定义的,不妨令 f′(xt)⋅Δ=−(f′(xt))2 ,此时 Δ=−f′(xt),又因为误差,我们不希望 Δ 过大,可以再加入学习率 η 来限制,此时
x_{t+1}=x_{t}+\Delta=x_{t}-\eta f^\prime(x_{t})$$此时再将 $f(x)$ 在 $x_{t+1}$ 处近似展开,继续求得 $x_{t+2}$ 的值,不断迭代更新。