一种无监督学习方法，通过无标签的训练样本，学习数据潜在规律，将数据集中的样本划分为多个不相交的子集（簇 cluster），每个子集可能会对应一个潜在的概念，为进一步数据分析提供基础。

聚类是个模糊且庞大的算法，几个常见的聚类模型：

质心聚类（原型聚类）：每个聚类由一个中心向量表示，可以不属于数据集。
密度聚类：聚类被定义为密度高于数据集其余部分的区域，稀疏区域中的对象通常被认为是噪声和边界点。
分布模型聚类：被定义为最有可能属于同一分布的对象。这种方法可以捕获属性之间的相关性和依赖性，但对于许多真实数据集，可能没有简明定义的数学模型.
连通性聚类：根据一个样本附近样本的相似性，将他们连接起来，所有连在一起的样本被认为是一个簇

算法

k-means

是一种质心聚类。给定数据集 $D$ ，需要 $k$ 个原型（均值向量） $\mu=\{\mu_{1},\dots,\mu_{k}\}$ ，来划分为 $k$ 个簇 $C=\{C_{1},\dots C_{k}\}$ 。
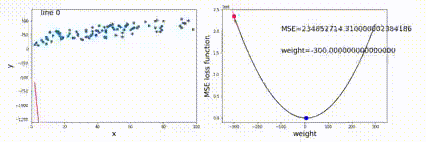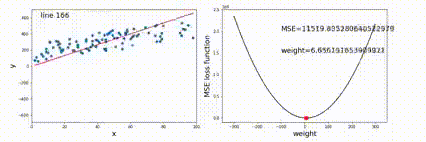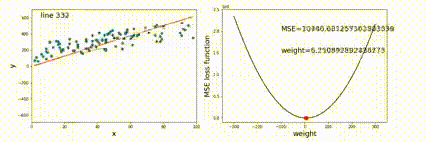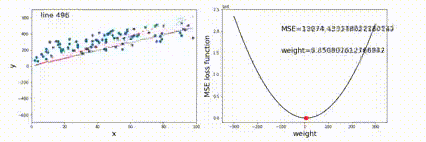
目标是： $\min_{\mu}\sum^n_{i} \sum_{x \in C_{i}} {||x-\mu_{j}||}^2$ ，是个非凸NP问题，只能通过迭代下降近似得到一个局部最优解

优化过程伪代码完整代码：

dataset:list # D={x_1,...,x_n}
k:int  # 给定 k 个簇

def distance(a:vector,b:vector)->scalar:...  # 计算向量 a 与 b 之间的距离


# 从数据集中随机无放回的随机采样 k 个样本作为原型  
rand_idx = random.sample(range(len(dataset)), k)  
prototypes = [dataset[idx] for idx in rand_idx]

while True:  
    clusters: list[list[np.ndarray]] = [[] for _ in range(k)]  # k个簇，初始为空  
  
    # step: 计算簇  
    for sample in dataset:  
        d = [distance(sample, prototypes[j]) for j in range(k)]  # 计算该样本与各原型的距离  
        idx = d.index(min(d))  # 取得与该样本距离最小的原型下标  
        clusters[idx].append(sample)  # 将该样本放入距离最小原型对应的簇中  
  
    # step: 更新原型  
    updated = False  
    for i in range(k):  
        prototype: np.ndarray = np.average(clusters[i], axis=0)  # 计算新的原型  
        if all(prototype != prototypes[i]):  # 如果原型有变化  
            updated = True  
            prototypes[i] = prototype  # 更新原型  
    print(prototypes)  
    if not updated:  # 如果所有原型都没有变化  
        return prototypes  # 如果原型均没有更新，则说明收敛。

缺点

对原型的初始化比较敏感，且只能得到局部最优，所以通常需要使用多个不同的初始化原型，选取效果最好的一个。
根据与原型的距离，根据距离来讲数据分为球状类的簇，这导致对于非凸的数据效果不好。

变种

kmeans++：优化了初始原型的选择，尽量选择相距较远的样本点作为初始原型，能一定程度上避免陷入局部最优。
k-medians 将原型更新为平均数改为更新为中位数，k-medoids 将原型更新改为选择数据集中的样本。
fuzzy c-means：不再明确将样本划分为某个簇，而是通过隶属度来表示属于某个簇的程度。

高斯混合聚类

是一种分布模型聚类。
多元高斯分布的概率密度函数（模型）：

p(x|\mu,\Sigma)=\frac{1}{(2\pi)^{\frac{n}{2}}{|\Sigma|}^{\frac{1}{2}}}e^{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)} \tag{1}

$\mu \in \mathbb{R}^n$ 是均值向量， $\Sigma\in\mathbb{R}^{n \times n}$ 是协方差矩阵。混合高斯分布（混合模型）：

p_{M}(x)=\sum^k_{i}\alpha_{i} \cdot p(x|\mu_{i},\Sigma_{i}) \tag{2}

后验分布， $z_i=j$ 表示样本 $x_{i}$ 由第 $j$ 个模型生成：

p_{M}(z_{i}=j|x_{i})=\frac{\alpha_{j}\cdot p(x_{i}|\mu_{i},\Sigma_{i})}{\sum^k_{l=1}\alpha_{l} \cdot p(x_{i}|\mu_{l},\Sigma_{l})}\tag{3}

显然我们无法直接极大似然，因为我们无法知道某个样本点属于哪个簇（子模型），需要以迭代的方式近似估计，通常使用 EM 算法。

使用极大对数似然估计参数值，

\begin{aligned} LL(D)&=\ln\left( \prod^m_{i=1}P_{M}(x_{i}) \right) \\ &=\sum^n_{i=1}\ln P(x_{i}) \\ &=\sum^n_{i=1}\ln\left( \sum^k_{j=1}\alpha_{j} \cdot p(x_{i}|\mu_{j},\Sigma_{j}) \right) \end{aligned}

求导置零

\begin{aligned} \frac{ \partial LL(D) }{ \partial \mu_{j} }&=0\\ \sum^n_{i} \frac{\alpha_{j}\cdot p(x_{i}|\mu_{j},\Sigma_{j})}{\sum^k_{l}\alpha_{l} \cdot p(x_{i}|\mu_{l}.\Sigma_{l})}(x_{i}-\mu_{j})&=0 \\ \mu_{j}= \frac{\sum^n_{i=1}p_{M}(z_{i}=j|x_{i})x_{i}}{\sum^n_{i=1}p_{M}(z_{i}=j|x_{i})} \end{aligned}\tag{4}

即混合成分的均值可通过样本加权平均来估计。由 $\frac{ \partial LL(D) }{ \partial \Sigma_{i} }=0$ 得：

\Sigma_{j}=\frac{\sum^n_{i} p_{M}(z_{i}=j|x_{i})(x_{i}-\mu_{j})(x_{i}-\mu_{j})^T}{\sum^n_{i} p_{M}(z_{i}=j|x_{i})} \tag{5}

对于 $\alpha_{j}$ 还需要满足约束 $a_{j}\geq 0,\sum^k_{j}\alpha_{j}=1$ ，对拉格朗日形式 $LL+\lambda\left( \sum^k_{j=1}\alpha_{j}-1 \right)$ 求导置 $0$ ：

\sum^n_{i=1} \frac{p(x_{i}|\mu_{j},\Sigma_{j})}{\sum^k_{l=1}\alpha_{l} \cdot p(x_{i}|\mu_{l}.\Sigma_{l})}=-\lambda

两别同乘以 $\alpha_{j}$ :

\sum^n_{i=1} \frac{\alpha_{j} p(x_{i}|\mu_{j},\Sigma_{j})}{\sum^k_{l=1}\alpha_{l} \cdot p(x_{i}|\mu_{l}.\Sigma_{l})}=-\lambda\alpha_{j}

两边再对所有混合成分求和：

\begin{aligned} \sum^k_{j=1}\sum^n_{i=1} \frac{\alpha_{j} p(x_{i}|\mu_{j},\Sigma_{j})}{\sum^k_{l=1}\alpha_{l} \cdot p(x_{i}|\mu_{l}.\Sigma_{l})}&=-\sum^k_{j=1}\lambda\alpha_{j}\\ \sum^n_{i=1} \frac{\sum^k_{j=1}\alpha_{j} p(x_{i}|\mu_{j},\Sigma_{j})}{\sum^k_{l=1}\alpha_{l} \cdot p(x_{i}|\mu_{l}.\Sigma_{l})}&=-\lambda\sum^k_{j=1}\alpha_{j}\\ \sum^n_{i=1}1&=-\lambda\cdot 1\\ n&=-\lambda \end{aligned}\tag{6}

因此：

\begin{aligned} \sum^n_{i=1} \frac{\alpha_{j} p(x_{i}|\mu_{j},\Sigma_{j})}{\sum^k_{l=1}\alpha_{l} \cdot p(x_{i}|\mu_{l}.\Sigma_{l})}&=n\alpha_{j} \\ a_{j}&=\frac{1}{n}\sum^n_{i=1} \frac{\alpha_{j} p(x_{i}|\mu_{j},\Sigma_{j})}{\sum^k_{l=1}\alpha_{l} \cdot p(x_{i}|\mu_{l}.\Sigma_{l})} \\ a_{j}&=\frac{1}{m}\sum^n_{i}p_{M}(z_{i}=j|x_{i}) \end{aligned}\tag{7}

此时可以使用 EM 算法：

n:int  # 样本数
k:int  # 模型（簇）数
dataset:list[vector]  # 数据集
# k 个模型，每个模型由 (权重alpha,均值向量，协方差矩阵）确定，先随机初始化。
models:list[tulple[float,vector[n],matrix[n,n]]]=[(rand,rand,rand)*k]

threshold:float = 0.001  # 阈值，如果变化小于这个数，则说明模型收敛停止训练

pp(index:int,sample:vector,model:list)->float:...  # 计算后验分布，式(3)
mu(index:int,dataset:list[vector])->vector:...  # 通过极大似然 计算mu，式(4)
sigma(index:int,dataset:list[vector])->matrix:...  # 通过极大似然 计算sigma，式(5)
sigma(index:int,dataset:list[vector])->float:...  # 通过极大似然 计算 alpha,式(7)
while True:
	# 首先计算此时每个样本属于每个模型的概率
	y:matrix[n,k]
	for i in range(n):
		for j in range(k):
			y[i,k] = pp(j,dataset[i],models)
	new_models = models
	for i in range(k): 
		 new_models[i] = (alpha(i,dataset),mu(i,dataset),sigma(i,dataset)) 
		 alpha[i] = 
	# 如果模型更新变化小于阈值，则说明收敛，停止训练
	if models-new_models<threshold:
		break
	else 
		models = new_models

缺陷：

多次运行可能会产生不同的结果
对于许多真实数据集，可能没有简明定义的数学模型并不是服从高斯分布的

DBSCAN

一种密度聚类算法

dataset:list[vector]  # 数据集
unvisited:list[vector] = dataset  # 未访问过的点
eps:float  # 邻域大小
M:int  # 如果一个样本点的领域内存在大于 M 个样本，则创建一个新的簇
clusters:list[vector]  # 簇
noise:list[vector]  # 噪声

get_near_samples(object:vector,dataset:list,eps:float)  # 获取 object 邻域内的点。

while not unvisited.empty():
	sample = unvisited[rand(len(unvisited))]  # 随机选区一个未访问过的对象
	unvisited.remove(sample)
	# 获取样本点 eps 邻域内的样本点
	near_samples = get_near_samples(sample,dataset,eps)
	if len(near_samples) > M:
		# 如果邻域密度符合，创建一个新的簇
		cluster=[sample]
		# 遍历邻域内所有样本点
		for near_sample in near_samples:
			unvisited.remove(near_sample)
			cluster.append(near_sample)
			if len(get_near_samples(near_sample,dataset))>0:
				# 如果邻域内样本点的邻域满足密度条件，则将其也加入新的簇
				cluster+=get_near_samples(near_sample,dataset)
		clusters.append(cluster)
	else:
		noise.append(sample)

缺陷

由于它们期望某种密度下降来检测簇边界，在具有高斯分布（人工数据中的常见用例）的数据集上效果不好，因为聚类密度不断降低，无法有效的确定边界。

变体

OPTICS：是DBSCAN的推广，无需为范围参数 ε 选择合适的值，并产生与连锁聚类相关的分层结果，但是仍然存在DBSCAN的缺陷
Density-Link-Clustering：结合了单链接聚类和 OPTICS 的思想，完全消除了 ε 参数，并通过使用 R 树索引提供了优于 OPTICS 的性能改进。

性能度量

聚类结果的评估与聚类本身一样困难。
两种方式：

外部评估：使用现有的 ground truth 分类进行比较，即使用带标签的数据。但是标签仅反应了数据一种可能的分区，并不意味着不存在不同甚至更好的聚类。
内部评估：通过簇内相似度、不同簇的相似度等特征来评估好坏。